Question

What is the area (in square units) of the region under the curve of the function f(x)=x+3, on the interval from x=1 to x=3 ?

Answer 1

10 square units

Explanation:

We want to find the area under the curve
`f(x)=x+3` from x=1 to x=3.

We use definite integrals to find this area.

`\int\limits^3_1 {x+3} \, dx`

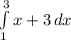
We integrate to obtain:

`(x^2)/(2)+3x|_1^3`

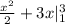
We evaluate the limits to get:

`(3^2)/(2)+3(3)-((1^2)/(2)+3(1))`

`4.5+9-0.5-3=10`

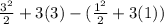
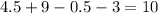
Therefore the area under the curve from x=1 to x=3 is 10 square unit.