2 Answers

Mike Yang · Answer 1 · 2020-05-23T03:40:23+0000

|x-4| <3

=>. x-4<3 or -(x-4)<3

=>. x-4<3 or x+4>3

=>. x<7 or x>1

So solution is x>1 & x<7. =x€(1,7)

Hope it helps...

Regards,

Leukonov/Olegion.

Sul Aga · Answer 2 · 2020-05-24T18:42:00+0000

Answer:

The solution to the given inequality is:

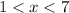1<x<7 i.e. in the interval form it is given by: (1,7)

We are given a inequality in term of variable x as follows:

|x-4|<3

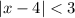
Now, we know that any inequality with modulus function is opened as follows:

If

|x-a|<b

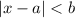
Then we have:

-b<x-a<b

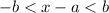
i.e. we may write it as:

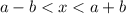
a-b<x<a+b

Here in the given expression we have:

a=4 and b=3

Hence, the solution is given by:

$4-3<x<4+3\\\\i.e.\\\\1<x<7$