Question

X+2y=7 x-2y=-1 what is solution

Answer 1

It's a system of linear equations; let me write it out more neatly for you:

`\left \{ {x + 2y = 7} \atop {x - 2y = -1}} \right.`

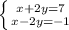
Good. In order to solve a system of equations with two variables, we can find one variable and then use that variable to find the other. This wouldn't be the case if we just had one equation, note.

Let's work on the top one first. There's multiple ways of solving this one, but here's the most simple way: isolating a single variable. The goal is to get either just x or just y on one side.

`x + 2y=7\\x = 7-2y`

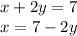
Nice. Now that we have a value of x, we can just plug it into the other equation -- since we know that x is equal to another expression, we can replace x in the other equation with the expression.

`x - 2y = -1\\(7-2y)-2y = -1\\7 - 2y - 2y = -1\\7 - 4y = -1 \\-4y = -8\\y = 2`

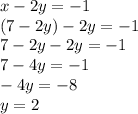
Now that we have y, we can do the same thing for x. This time, however, we have the actual value of y, meaning we can just plug that in.

`x = 7 - 2y\\x = 7 - 2(2)\\x = 7 - 4 \\x = 3`

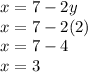
Our solution is

`\left \{ {{x=3} \atop {y=2}} \right.`

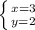
We can check this by plugging the values back into the equation.

`3 + 2(2) = 7\\3 + 4 = 7`

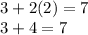
and

`3 - 2(2) = -1\\3 - 4 = -1\\`

That's it. There's another (easier) way to handle this specific equation, but this is the simplest way to do it.

Answer 2

x=3,y=2

lkajsdfvnkkkkkk