Question

Assume there is a 50% chance of having a boy. Find the probability of

exactly two boys in three births.

Answer 1

0.375

Explanation:

Given that there is 50% chance of having a boy in a single birth.

Let it be represented by p, so

p=50%=0.5

According to Bernoulli's theorem, the probability of exactly r success in n trials is

`P(r)=\binom {n}{ r} p^r(1-p)^(n-r)`

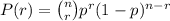
where p is the probability of success.

So, the probability of exactly 2 boys (success) in a total of 3 birth (trials) is

`P(r=2)=\binom {3}{ 2} p^2(1-p)^(3-2)`

As p=0.5, so

`P(r=2)=\binom {3}{ 2} (0.5)^2(1-0.5)^(3-2) \\\\=\binom {3}{2} (0.5)^2(0.5)^(1) \\\\=3* 0.5^3`

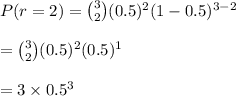
=0.375

Hence, the probability of exactly 2 boys in a total of 3 birth is 0.375.