Question

There are 5 boys and 5 girls on a co-ed basketball team. A team plays 5 players on the court at one time, and the team can have at most 3 boys. How many possible teams can be created?

Answer 1

226 teams

Explanation:

A team can be:

• 5 girls
• 4 girls and 1 boy
• 3 girls and 2 boys
• 2 girls and 3 boys

Count all combinations:

1. 5 girls from 5 girls can be chosen in 1 way.

2. 4 girls from 5 girls can be chosen in

`C^5_4=(5!)/(4!(5-4)!)=(1\cdot 2\cdot 3\cdot 4\cdot 5)/(1\cdot 2\cdot 3\cdot 4\cdot 1)=5`

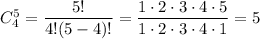
different ways and 1 boy from 5 boys can be chosen in

`C^5_1=(5!)/(1!(5-1)!)=(5!)/(1!\cdot 4!)=(1\cdot 2\cdot 3\cdot 4\cdot 5)/(1\cdot 2\cdot 3\cdot 4\cdot 1)=5`

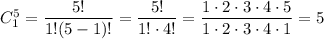
different ways, so in total,

`5\cdot 5=25`

different combinations.

3. 3 girls from 5 girls can be chosen in

`C^5_3=(5!)/(3!(5-3)!)=(5!)/(3!\cdot 2!)=(1\cdot 2\cdot 3\cdot 4\cdot 5)/(1\cdot 2\cdot 3\cdot 1\cdot 2)=10`

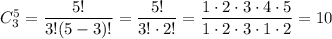
different ways and 2 boys from 5 boys can be chosen in

`C^5_2=(5!)/(2!(5-2)!)=(5!)/(2!\cdot 3!)=(1\cdot 2\cdot 3\cdot 4\cdot 5)/(1\cdot 2\cdot 1\cdot 2\cdot 3)=10`

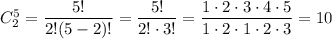
different ways, so in total,

`10\cdot 10=100`

different combinations.

4. 2 girls from 5 girls can be chosen in

`C^5_2=(5!)/(2!(5-2)!)=(5!)/(2!\cdot 3!)=(1\cdot 2\cdot 3\cdot 4\cdot 5)/(1\cdot 2\cdot 1\cdot 2\cdot 3)=10`

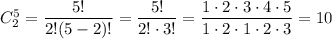
different ways and 3 boys from 5 boys can be chosen in

`C^5_3=(5!)/(3!(5-3)!)=(5!)/(3!\cdot 2!)=(1\cdot 2\cdot 3\cdot 4\cdot 5)/(1\cdot 2\cdot 3\cdot 1\cdot 2)=10`

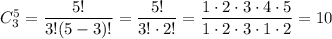
different ways, so in total,

`10\cdot 10=100`

different combinations.

In total, there are

`1+25+100+100=226`

possible teams.