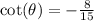Question

Angle θ is in standard position. If (8, -15) is on the terminal ray of angle θ, find the values of the trigonometric functions.

Answer 1

sin=-15/17

cos=8/7

tan=-15/8

csc=-17/15

sec=17/8

cot=-8/15

Answer 2

`\sin( \theta) = - (15)/(17)`

`\csc( \theta) = - (17)/(15)`

`\cos( \theta) = (8)/(17)`

`\sec( \theta) = (17)/(8)`

`\tan( \theta) = - (15)/(8)`

`\cot( \theta) = - (8)/(15)`

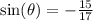
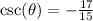
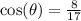
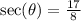
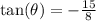
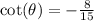
Step-by-step explanation

From the Pythagoras Theorem, the hypotenuse can be found.

`{h}^(2) = 1 {5}^(2) + {8}^(2)`

`{h}^(2) = 289`

`h = √(289)`

`h = 17`

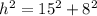
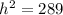
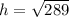
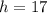
The sine ratio is negative in the fourth quadrant.

`\sin( \theta) = - (opposite)/(hypotenuse)`

`\sin( \theta) = - (15)/(17)`

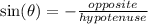
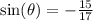
The cosecant ratio is the reciprocal of the sine ratio.

`\csc( \theta) = - (17)/(15)`

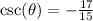
The cosine ratio is positive in the fourth quadrant.

`\cos( \theta) = (adjacent)/(hypotenuse)`

`\cos( \theta) = (8)/(17)`

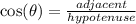
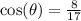
The secant ratio is the reciprocal of the cosine ratio.

`\sec( \theta) = (17)/(8)`

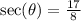
The tangent ratio is negative in the fourth quadrant.

`\tan( \theta) = - (opposite)/(adjacent)`

`\tan( \theta) = - (15)/(8)`

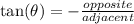
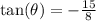
The reciprocal of the tangent ratio is the cotangent ratio

`\cot( \theta) = - (8)/(15)`