Question

Dont do QA
plzzzzzzzzzzzzzzzzzzzzzzzz

Answer 1

`(a) x^2-2x=x * (x+2) \\\\(b) 6x^2+12x=2* 3 * x * ( x + 2) \\\\(c) 3x^3 - 9x=3* x * (x^2 -3) \\\\(d) 4x^2 +28 x^3 = 2 * 2 * x * x * ( 1+ 7x)`

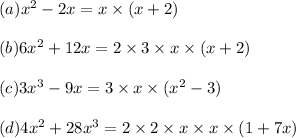
Explanation:

To factorize, at first, do factorize all the terms then take the common terms out.

(a)
`x^2-2x`

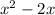
This can be written as

`x^2-2x= x* x + 2 * x`

Now, taking x commom from both the terms.

`x^2-2x=x * (x+2)`

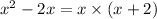
(b)
`6x^2+12x`

`=2* 3 * x* x + 2* 2 * 3 * x`

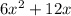
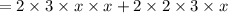
Now, taking
`2* 3* x` common from both the terms, we have

`6x^2+12x=2* 3 * x * ( x + 2)`

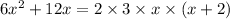
This is the required factorization.

(c)
`3x^3 - 9x \\\\`

`= 3 * x * x * - 9* x \\\\ 3x^3 - 9x=3* x * (x^2 -3)`

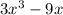
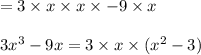
This is the required factorization.

(d)
`4x^2 +28 x^3`

`= 2 * 2 * x * x + 2 * 2 * 7 * x * x * x \\\\4x^2 +28 x^3 = 2 * 2 * x * x * ( 1+ 7x)`

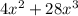
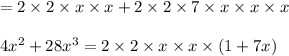
This is the required factorization.