Question

Which linear inequality is represented by the graph?

Answer 1

y < 6/4x - 3

Explanation:

Answer 2

The required inequality is
`y<(2)/(3)(x)-1`.

Explanation:

From the given graph it is clear that the related line passes through the points (-3,-3) and (3,1).

If a line passes through two points, then the equation of line is

`y-y_1=(y-y_1)/(x-x_1)(x-x_1)`

The equation of related line is

`y-(-3)=(1-(-3))/(3-(-3))(x-(-3))`

`y+3=(4)/(6)(x+3)`

`y+3=(2)/(3)(x+3)`

`y+3=(2)/(3)(x)+2`

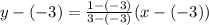
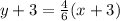
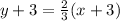
Subtract 3 from both the sides.

`y=(2)/(3)(x)+2-3`

`y=(2)/(3)(x)-1`

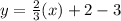
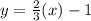
The equation of related line is
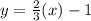`y=(2)/(3)(x)-1`. The related line is a dotted and the shaded region is below the line. So, the sign of inequality is <.

The required inequality is

`y<(2)/(3)(x)-1`

Therefore the required inequality is
`y<(2)/(3)(x)-1`.