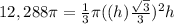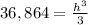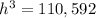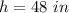Answer:
The height of the cone is
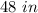
Explanation:
step 1
Find the radius of the base of cone
we know that
The volume of the cone is equal to
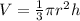
we have

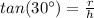 ---> remember that the vertex angle of the vertical cross section is 60 degrees
---> remember that the vertex angle of the vertical cross section is 60 degrees
so
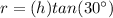
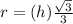
substitute the values and solve for h