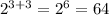Question

40 POINTS

Simplifying exponents and rules of exponents simplify the expressions below:

2 4 3 0 4 6 4 -3 2 3 2

Answer 1

a. 16

b. 1

c. 64

d. 64

Step-by-step explanation

We want to simplify the following exponential expressions

a.

`{2}^(4)`

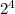
This implies that

`{2}^(4) = 2 * 2 * 2 * 2`

`{2}^(4) = 16`

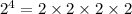
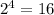
b. Any non-zero number exponent zero is 1.

This implies that,

`{3}^(0) = 1`

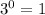
c. The given exponentiial expression is,

`{4}^(6) * {4}^( - 3)`

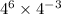
The bases are the same so we add the exponents.

`{4}^(6) * {4}^( - 3) = {4}^(6 + - 3)`

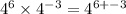
This simplifies to,

`{4}^(6) * {4}^( - 3) = {4}^(3)`

`{4}^(6) * {4}^( - 3) = 4 * 4 * 4 = 64`

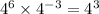
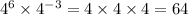
d. We want to simplify:

`{ ({2}^(3)) }^(2)`

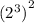
This is the same as

`{ ({2}^(3)) }{ ({2}^(3)) }`

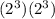
We add the exponents now to get:

`{2}^(3 + 3) = {2}^(6) = 64`