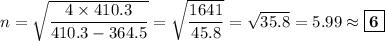Question

Determine the Balmer formula n and m values for the wavelength 656.5 nm. Possible Choices: m= 1 n= 2 m= 2 n= 3 m= 3 n= 4 m= 2 n= 5 Part B Determine the Balmer formula n and m values for the wavelength 486.3 nm. Possible Choices: m= 1 n=2 m= 2 n=3 m= 1 n=4 m= 2 n=4 Part C Determine the Balmer formula n and m values for the wavelength 434.2 nm. Possible Choices: m= 1 n= 4 m= 2 n= 4 m= 3 n= 4 m= 2 n= 5 Part D Determine the Balmer formula n and m values for the wavelength 410.3 nm. Possible Choices: m= 2 n= 4 m= 2 n= 5 m= 3 n= 4 m= 2 n= 6

Answer 1

`\boxed{\text{A. } m = 2, n = 3; \text{B. } m = 2, n = 4; \text{C. } m = 2, n = 5; \text{D. } m = 2, n = 6}`

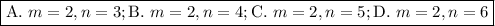
Step-by-step explanation:

The Balmer equation is

`\lambda = B\left((n^(2))/(n^(2) -m^(2))\right)`

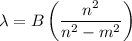
where B = 364.5 nm and m = 2

Thus, the Balmer equation reduces to

`\lambda = 364.5\left((n^(2))/(n^(2) - 4)\right)`

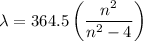
We will be doing four separate calculations for n, so it will be convenient to solve the equation for n.

`\lambda (n^(2) -4) = 364.5n^(2)\\\\\lambda n^(2) -4\lambda = 364.5n^(2)\\\\\lambda n^(2)- 364.5n^(2) = 4\lambda \\\\ n^(2)(\lambda - 364.5) = 4\lambda \\\\ n^(2)= (4\lambda)/(\lambda - 364.5)\\\\ n= \sqrt{(4\lambda)/(\lambda - 364.5)}`

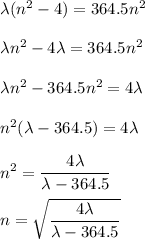
A. λ = 656.5 nm

`n= \sqrt{(4 * 656.5)/(656.5 - 364.5)} = \sqrt{(2626)/(292)} =√(8.993) = 2.999 \approx \boxed{\mathbf{3}}`

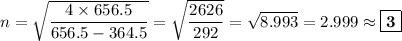
B. λ = 486.3 nm

`n= \sqrt{(4 * 486.3)/(486.3 - 364.5)} = \sqrt{(1945)/(121.8)} =√(15.97) = 3.996 \approx \boxed{\mathbf{4}}`

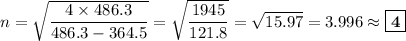
C. λ = 434.2 nm

`n= \sqrt{(4 * 434.2)/(434.2 - 364.5)} = \sqrt{(1737)/(69.7)} =√(24.9) = 4.99 \approx \boxed{\mathbf{5}}`

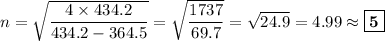
D. λ = 410.3 nm

`n= \sqrt{(4 * 410.3)/(410.3 - 364.5)} = \sqrt{(1641)/(45.8)} =√(35.8) = 5.99 \approx \boxed{\mathbf{6}}`