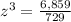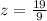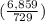Question

42. What is the surface area of a sphere with a circumference of 50 feet round the answer to the nearest 10th.

43. The volume of a sphere is 2254 pi m^3. What is the surface of the sphere to the nearest 10th?

44. What is the scale factor of a cube with a volume of 729 m^3 to a cube with a volume of 6859?

Answer 1

Part 42) The surface area of the sphere is
`SA=795.8\ ft^(2)`

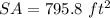
Part 43) The surface area of the sphere is
`SA=1,781.6\ m^(2)`

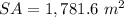
Part 44) The scale factor is
`(19)/(9)`

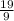
Explanation:

Part 42) What is the surface area of a sphere with a circumference of 50 feet round the answer to the nearest 10th

step 1

Find the radius of the sphere

The circumference is equal to

`C=2\pi r`

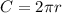
we have

`C=50\ ft`

assume

`\pi =3.14`

substitute and solve for r

`50=2(3.14)r`

`r=7.96\ ft`

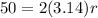
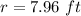
step 2

Find the surface area of the sphere

The surface area of the sphere is equal to

`SA=4\pi r^(2)`

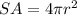
substitute the value of r

`SA=4(3.14)(7.96)^(2)`

`SA=795.82\ ft^(2)`

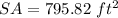
round to the nearest 10th

`795.82=795.8\ ft^(2)`

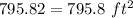
Part 43) The volume of a sphere is 2254 pi m^3. What is the surface of the sphere to the nearest 10th?

step 1

Find the radius of the sphere

The volume of the sphere is equal to

`V=(4)/(3)\pi r^(3)`

we have

`V=2,254\pi\ m^(3)`

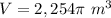
substitute and solve for r

`2,254\pi=(4)/(3)\pi r^(3)`

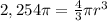
Simplify

`1,690.5=r^(3)`

`r=11.91\ m`

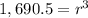
step 2

Find the surface area of the sphere

The surface area of the sphere is equal to

`SA=4\pi r^(2)`

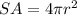
substitute the value of r

`SA=4(3.14)(11.91)^(2)`

`SA=1,781.6\ m^(2)`

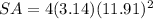
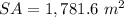
Part 44) What is the scale factor of a cube with a volume of 729 m^3 to a cube with a volume of 6859?

we know that

If two figures are similar, then the ratio of its volumes is equal to the scale factor elevated to the cube

so

Let

z -----> the scale factor

x ----> the volume of the larger cube

y ----> the volume of the smaller cube

`z^(3)=(x)/(y)`

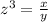
we have

`x=6,859\ m^(3)`

`y=729\ m^(3)`

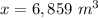
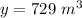
substitute

`z^(3)=(6,859)/(729)`

`z=(19)/(9)`

`((6,859)/(729))`