Question

The height of right circular cylinder P

is twice the height of right circular
cylinder Q. The radii of the cylinders are
of equal length
What number times the volume of
cylinder Q is equal to the volume of
cylinder P?
A. 2
B. 4
C. 6
D. 8

Answer 1

A. 2

Explanation:

The computation is shown below:

As we know that

The Volume of a right circular cylinder is

`V = \pi r^h\\\\`

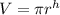
Here r is the radius

And h is the height

Now it is mentioned that the height of the right circular cylinder P is double to the height of the right circular cylinder Q

Now let us assume h be the height of cylinder p

And, H be the height of cylinder Q

So the equation is

h = 2H ........(1)

Also

The radius of both the cylinders would be the similar length

So

we assume the r be the radius of both cylinders

Now

The Volume of cylinder Q =
`V_Q = \pi r^2H`

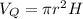
And for P it is
`V_p = \pi r^2 h`

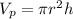
Now substitute equation 1

`V_p = \pi r^2(2H)\\\\V_p= 2 \pi r^2hH\\\\V_p = 2(\pi r^2H)\\\\V_p = 2(V_Q)`

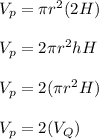
Hence, the correct option is A.