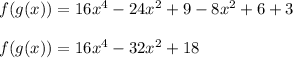Question

Please HELP ASAP I really need help

Answer 1

`f(g(x)) = 16 {x}^(4) -3 2{x}^(2) +18`

EXPLANATION

The given functions are:

`f(x)={x}^(2) - 2x + 3`

and

`g(x) = 4 {x}^(2) - 3`

We want to find

`f(g(x)) = f(4 {x}^(2) - 3)`

This implies that;

`f(g(x)) = ( 4 {x}^(2) - 3)^(2) - 2(4 {x}^(2) - 3) + 3`

We expand to get,

`f(g(x)) = 16 {x}^(4) - 24 {x}^(2) + 9- 8 {x}^(2) + 6+ 3`

`f(g(x)) = 16 {x}^(4) -3 2{x}^(2) +18`

Answer 2

`f(g(x)) = 16x ^ 4-32x ^ 2 + 18`

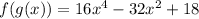
Explanation:

we have two functions

`f (x) = x ^ 2 -2x + 3\\\\g (x) = 4x ^ 2-3`

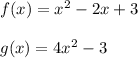
We wish to find the compound function f(g(x))

To find f(g(x)) you must introduce the function g(x) within the function f(x). This is change the variable x, in the function f(x), by g(x).

`f (g (x)) = (4x ^ 2-3) ^ 2 - 2 (4x ^ 2-3) +3`

Now simplify the expression:

`f (g (x)) = 16x ^ 4-24x ^ 2 + 9 - 8x ^ 2+6 +3\\\\f(g(x)) = 16x ^ 4-32x ^ 2 + 18`