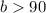Question

Please help! John-Mark recorded the stats for several baseball pitchers. He made a scatterplot showing the

number of games they played and the percentage they lost. Which line is the best fit for this
data?

y = 10x - 70
y = 10x + 70
y = -10x + 110
y = -10x - 110​

Answer 1

Answer: Third Option

`y = -10x + 110`

Explanation:

The equation of a line in the pending intersection form has the following form:

`y=mx +b`

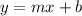
Where m is the slope of the line and b is the intersection with the y axis.

Observe in the graph that the data form a decreasing line. Then the adjustment line must have a negative slope
`m <0`.

The first and the second option have positive slopes, therefore we discard them.

Notice in the scatter diagram that the intersection of the line with the y-axis (x = 0) is above 90.

The line of the fourth option has a value of
`b = -110 <90`.

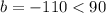Therefore the line that best fits the data is the third option

`y = -10x + 110`

Note that the line has a slope
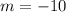`m = -10` and a value of
`b> 90`