Question

Suppose θ is an angle in the standard position whose terminal side is in Quadrant IV and . Find the exact values of the five remaining trigonometric functions of θ.

Answer 1

If
`\theta` falls in quadrant IV, then we know
`\sin\theta<0` and
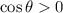`\cos\theta>0`. By definition of cosecant,

`\csc\theta=\frac1{\sin\theta}`

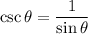
so we also know that
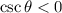`\csc\theta<0`. Recall that

`\cot^2\theta+1=\csc^2\theta`

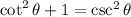
which means

`\csc\theta=-√(\cot^2\theta+1)=-\frac{√(10)}3`

`\implies\sin\theta=-\frac3{√(10)}`

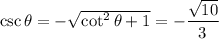
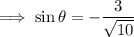
By definition of cotangent,

`\cot\theta=(\cos\theta)/(\sin\theta)\implies\cos\theta=\frac1{√(10)}`

`\implies\sec\theta=√(10)`

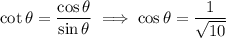
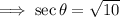
We also immediately know that

`\tan\theta=-\frac{21}7`

The listed answers are unsimplified relative to the ones we've come up with here, but with some manipulation we find

`\sin\theta=-\frac3{√(10)}=-(7\cdot3)/(7√(10))=-(21)/(√(490))`

`\cos\theta=\frac1{√(10)}=\frac7{7√(10)}=\frac7{√(490)}`

`\csc\theta=\frac1{\sin\theta}=-(√(490))/(21)`

`\sec\theta=\frac1{\cos\theta}=\frac{√(490)}7`

`\tan\theta=\frac1{\cot\theta}=-\frac{21}7`

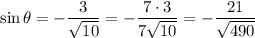
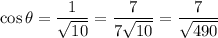
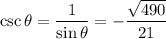
so that the third option is correct.