Question

Solve by substitution:
-5x + y = -2
-3x + 6y = -12

please explain

Answer 1

First we pick the equation. Let's say we pick first one. From it we express y.

`-5x+y=-2\Longrightarrow y=-2+5x`

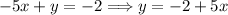
Then we use this y and plug it in instead of y in the second equation.

`-3x+6(-2+5x)=-12`

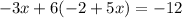
Now just solve for x.

`</p><p>-3x-12+30x=-12 \\</p><p>-3x=-30x \\</p><p>\underline{x=10}</p><p>`

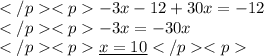
We plug this x in the first equation.

`-5\cdot10+y=-2`

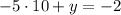
And solve for y.

`</p><p>-50+y=-2 \\</p><p>\underline{y=48}</p><p>`

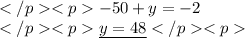
So the solution to the equation is geometrically a point P which lies on the intersection of the two lines.

`\boxed{P(10,48)}`

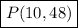
Hope this helps.

r3t40