Question

Y=4x^{2 -4x+9 Find the x-intercepts for the parabola

Answer 1

Answer: The parabola does not intercept the x-axis.

Explanation:

The parabola intercepts the x-axis when
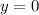`y=0`, then, you need to substitute
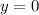`y=0` into the equation:

`y=4x^2 -4x+9\\0=4x^2 -4x+9`

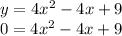
Now, use the Quadratic formula:

`x=(-b\±√(b^2-4ac))/(2a)`

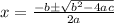
In this case:

`a=4\\b=-4\\c=9`

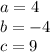
Substituting these values and evaluating, you get:

`x=(-(-4)\±√((-4)^2-4(4)(9)))/(2(4))\\\\x=(4\±√(-128))/(8)`

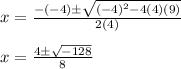
Remeber that:

`√(-1)=i`

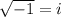
Then, rewriting:

`x=(4\±8i√(2))/(8)`

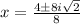
Simplifying:

`x=(4(1\±2i√(2))/(4(2))\\\\x=(1\±2i√(2))/(2)\\\\x=(1)/(2)\±(2i√(2))/(2)\\\\x=(1)/(2)\±i√(2)`

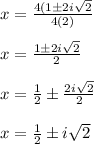
Then:

`x_1=(1)/(2)+i√(2)`

`x_2=(1)/(2)-i√(2)`

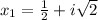
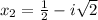
The roots are complex, therefore, the parabola does not intercept the x-axis.