ANSWER
circle
EXPLANATION
The given equation is
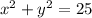
To determine the type of conic, we analyze the coefficient and sign of the quadratic terms.
If the coefficient of the quadratic terms are equal and have the same sign,then the conic is a circle.
If the coefficient of the quadratic terms are equal and have opposite signs,then the conic is a hyperbola.
If the coefficient of the quadratic terms are not equal and have the same sign,then the conic is an ellipse.
Since the coefficients are all 1 and the signs are positive, the given conic is a circle.