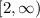ANSWER
Domain: All real numbers
Range:
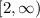
EXPLANATION
The given function is
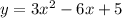
To find the domain and range of the given function, we complete the square.
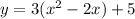
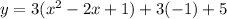
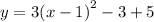
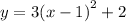
The vertex is at (1,2).
The given function is a polynomial and all polynomial functions are defined everywhere.
The domain is all real numbers.
The parabola opens upwards and have vertex at (1,2). Hence the minimum y-value is 2.
The range is