The inverse of the function
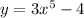 is
is
![y = \sqrt[5]{(x + 4)/(3)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wt72bs8b7017j3d0eutvvv9533na1ljfyh.png)
How to determine the inverse of the function
From the question, we have the following parameters that can be used in our computation:
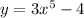
Swap the variabls x and y
So, we have

Add 4 to both sides
This gives

Divide through by 3

Take the 5th root of both sides
![y = \sqrt[5]{(x + 4)/(3)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wt72bs8b7017j3d0eutvvv9533na1ljfyh.png)
hence, the inverse of the function is
![y = \sqrt[5]{(x + 4)/(3)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wt72bs8b7017j3d0eutvvv9533na1ljfyh.png)