Answer: 2.775%
Explanation:
Given: Mean :
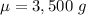
Standard deviation:
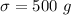
The formula to calculate z-score is given by :-

For x= 2,500g
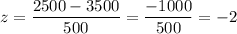
The p-value of z = P(z<-2)=0.02275
In percent,
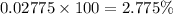
The percent of babies born in the United States are classified as having a low birth weight (< 2,500 g) = 2.775%