Question

Please help me out please

Answer 1

V = 400

Explanation:

The volume (V) of the pyramid is

V =
`(1)/(3)` area of base × perpendicular height (h)

Consider a right triangle from the vertex to the midpoint of the base across to the slant height, with hypotenuse of 13

Using Pythagoras' identity on the right triangle, then

h² + 5² = 13²

h² + 25 = 169 ( subtract 25 from both sides )

h² = 144 ( take the square root of both sides )

h =
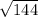`√(144)` = 12

Area of square base = 10² = 100, thus

V =
`(1)/(3)` × 100 × 12 = 4 × 100 = 400