ANSWER
0
EXPLANATION
The discriminant of a quadratic equation in the form
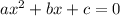
is given by
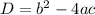
The discriminant of a quadratic equation tells us the nature of the roots of that quadratic equation.
If the discriminant is negative, the equation has no real roots.
If the discriminant us positive, the equation has two real roots.
If the discriminant is zero, the equation has a repeated root.
Since the discriminant is -6, the equation has no real roots.
In other words, the number of real roots is 0.