Question

Find a cubic function with the given zeros. 7, -3, 2 (1 point)

Answer 1

`f(x) =x^3-6x^2-13x+42`

Step-by-step explanation

The zeros of the cubic function is given as:

x=7,x=-3,x=2

This implies that, x-7,x+3,x-2 are factors of the given cubic polynomial function.

We can write the completely factored form as a function of x to get:

`f(x) = (x - 7)(x + 3)(x - 2)`

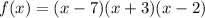
We expand to get:

`f(x) = (x - 7)(x^2+ x-6)`

`f(x) =x^3-6x^2-13x+42`

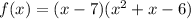
This is a cubic function because the highest degree is 3.