1 Answer

Jason Awbrey · Answer 1 · 2020-08-09T12:02:36+0000

According to the table,

$P(C\cap T)=\frac8{1000}$

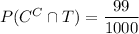
$P(C^C\cap T)=(99)/(1000)$

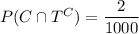
$P(C\cap T^C)=\frac2{1000}$

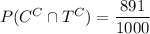
$P(C^C\cap T^C)=(891)/(1000)$

A. By the law of total probability,

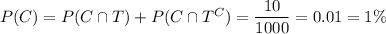
$P(C)=P(C\cap T)+P(C\cap T^C)=(10)/(1000)=0.01=1\%$

B. By definition of conditional probability,

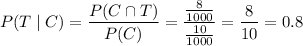
$P(T\mid C)=(P(C\cap T))/(P(C))=\frac{\frac8{1000}}{(10)/(1000)}=\frac8{10}=0.8$

That is, the test has an 80% probability of returning a true positive.

C. As in (B), we have by definition

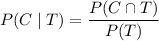
$P(C\mid T)=(P(C\cap T))/(P(T))$

but we don't yet know
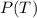P(T) . By the law of total probability,

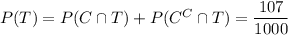
$P(T)=P(C\cap T)+P(C^C\cap T)=(107)/(1000)$

Then

$P(C\mid T)=\frac{\frac8{1000}}{(107)/(1000)}=\frac8{107}\approx0.075$

That is, the probability that a patient has cancer given that the test returns a positive result is about 7.5%.

D. Simply put, the events
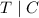$T\mid C$ and
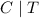$C\mid T$ are not the same, and the difference is derived directly from the fact that
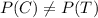$P(C)\\eq P(T)$ .

Please log in or register to add a comment.