Answer : The heat released is, 319.28 kJ
Solution :
The conversions involved in this process are :
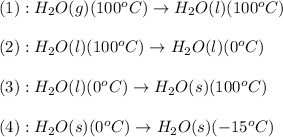
Now we have to calculate the enthalpy change.
![\Delta H=n* \Delta H_(condensation)+[n* c_(p,l)* (T_(final)-T_(initial))]+n* \Delta H_(freezing)+[n* c_(p,s)* (T_(final)-T_(initial))]](https://img.qammunity.org/2020/formulas/chemistry/high-school/sqiva2unbpoflqcpvfwjjpgfxkllbda8ko.png)
where,
 = enthalpy change = ?
= enthalpy change = ?
Mass of water = 105 g
Moles of water =
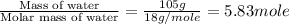
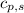 = specific heat of solid water =
= specific heat of solid water =
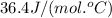
 = specific heat of liquid water =
= specific heat of liquid water =
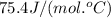
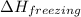 = enthalpy change for freezing = enthalpy change for fusion = - 6.01 KJ/mole = - 6010 J/mole
= enthalpy change for freezing = enthalpy change for fusion = - 6.01 KJ/mole = - 6010 J/mole
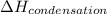 = enthalpy change for condensation = enthalpy change for vaporization = -40.67 KJ/mole = -40670 J/mole
= enthalpy change for condensation = enthalpy change for vaporization = -40.67 KJ/mole = -40670 J/mole
Now put all the given values in the above expression, we get
![\Delta H=5.83mole* -40670J/mole+[5.83mole* 75.4J/(mol.^oC)* (0-100)^oC]+5.83mole* -6010J/mole+[5.83mole* 36.4J/(mol.^oC)* (-15-0)^oC]](https://img.qammunity.org/2020/formulas/chemistry/high-school/5uewcvthau66qljce0jap6y8nxvm633g2l.png)
 (1 KJ = 1000 J)
(1 KJ = 1000 J)
Negative sign indicates that the heat is released during the process.
Therefore, the heat released is, 319.28 KJ