Question

Triangle FGH is an isosceles right triangle with a hypotenuse that measures 16 units. An altitude, , is drawn from the right angle to the hypotenuse. What is the length of ?

Answer 1

8 units

Explanation:

mid point of hypotenuse of right angled isosceles triangle is equidistant from three vertices.

length of altitude=16/2=8

Answer 2

The question is incomplete, here is a complete question.

Triangle FGH is an isosceles right triangle with a hypotenuse that measures 16 units. An altitude, GJ, is drawn from the right angle to the hypotenuse.

What is the length of GJ?

A. 2 units

B. 4 units

C. 6 units

D. 8 units

Answer : The correct option is, (D) 8 units

Step-by-step explanation :

Given:

Length FH = 16 unit

As we know that a altitude between the two equal legs of an isosceles triangle creates right angles is a angle and opposite side bisector.

Thus,

Length FJ = Length HJ =
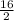`(16)/(2)` = 8 units

As, the triangle is an isosceles. So, length GF = length GH = x unit

First we have to determine the value of 'x'.

Using Pythagoras theorem in ΔFGH :

`(Hypotenuse)^2=(Perpendicular)^2+(Base)^2`

`(FH)^2=(GF)^2+(GH)^2`

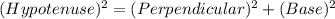
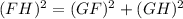
Now put all the values in the above expression, we get :

`(16)^2=(x)^2+(x)^2`

`256=2x^2`

`x^2=128`

`x=8√(2)`

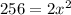
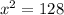
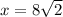
Thus, length GF = length GH = x unit =
`8√(2)`

Now we have to determine the length GJ.

Using Pythagoras theorem in ΔGJH :

`(Hypotenuse)^2=(Perpendicular)^2+(Base)^2`

`(GH)^2=(GJ)^2+(HJ)^2`

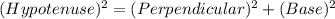
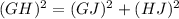
Now put all the values in the above expression, we get :

`(8√(2))^2=(GJ)^2+(8)^2`

`128=(GJ)^2+64`

`(GJ)^2=128-64`

`(GJ)^2=64`

`GJ=√(64)`

`GJ=8`

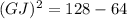
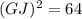
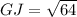
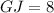
Thus, the length of GJ is, 8 units.