Answer:
Add 8 to both sides of the equation
Explanation:
We have been given the quadratic equation;
x^2 - 14x +41 = 0
we are required to complete the square in order to express it in the form;
(x - p)^2 = q
In order to do this we need to find a constant c, such that;
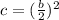
where b is the coefficient of x in the quadratic equation. In our case b = -14. Therefore,
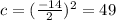
Therefore, for us to complete the square, the left hand side of the quadratic equation should be;
x^2 - 14x +49
Since we already have 41, we can simply add 8 to make it 49. Thus, the first correct step to write the above equation in the form (x - p)2 = 9, where p and q are integers is to Add 8 to both sides of the equation