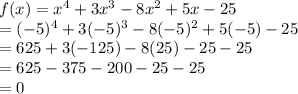Question

Match each polynomial function with one of its factors.

f(x) = x3 − 3x2 − 13x + 15

f(x) = x4 + 3x3 − 8x2 + 5x − 25

f(x) = x3 − 2x2 − x + 2

f(x) = -x3 + 13x − 12

x − 2 -->

x + 3 -->

x + 4 -->

x + 5 -->

Answer 1

See image

Explanation:

Plato/Edmentum

Answer 2

`x-2 => f(x)=x^(3)-2x^(2)-x+2\\x+3=>f(x)=x^(3)-3x^(2) -13x+15\\x+4=>f(x)=-x^(3)+13x-12\\x+5=>f(x)=x^(4)+3x^(3)-8x^(2)+5x-25`

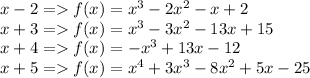
Explanation:

The value of a function will be zero if the factor is put in it. In order to check whether a factor is of a function or not we will put the value of x from that factor in the function:

So

x-2 = 0 => x=2

Putting in first function

`x^(3)-3x^(2) -13x+15\\=(2)^(3)-3(2)^(2) -13(2)+15\\=8-3(4)-26+15\\=8-12-26+15\\=23-38\\=-15 \\eq 0\\`

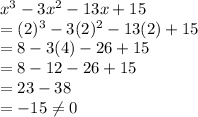
So x-2 is not a factor of first function.

Putting in second function

`f(x)=x^(4)+3x^(3)-8x^(2)+5x-25\\ =(2)^(4)+3(2)^(3)-8(2)^(2)+5(2)-25\\=16+3(8)-8(4)+10-25\\=16+24-32+10-25\\=-7\\eq 0`

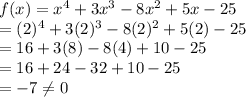
So x-2 is also not a factor of second function.

Putting in third function:

`f(x)=x^(3)-2x^(2)-x+2\\ =(2)^(3)-2(2)^(2)-2+2\\=8-2(4)-2+2\\=8-8-2+2\\=0`

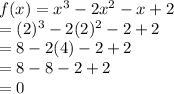
So x-2 is factor of third function.

...........................

For x+3

x+3=0

x=-3

First function:

`f(x)=x^(3)-3x^(2) -13x+15\\=(-3)^(3)-3(-3)^(2) -13(-3)+15\\=-27-3(9)+39+15\\=-27-27+39+15\\=-54+54\\=0\\`

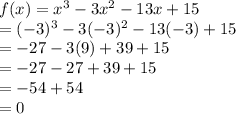
So x+3 is a factor of first function.

.............................

For x+4

x+4=0

x=-4

As we have already found the factors of first and third function, we will now only check second and fourth function.

`f(x)=x^(4)+3x^(3)-8x^(2)+5x-25\\ =(-4)^(4)+3(-4)^(3)-8(-4)^(2)+5(-4)-25\\=256+3(-64)-8(16)-20-25\\=256-192-128-20-25\\-109\\eq 0`

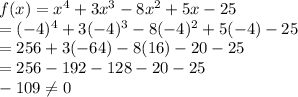
So x+4 is not a factor of second function.

Putting in fourth function:

`f(x)=-x^(3)+13x-12\\ =-(-4)^(3)+13(-4)-12\\=64-52-12\\=64-64\\=0\\`

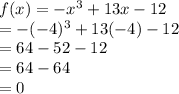
So x+4 is a factor of fourth function

..........................

For x+5=0

x=-5

Since only one function is remaining we'll only check for that.

`f(x)=x^(4)+3x^(3)-8x^(2)+5x-25\\ =(-5)^(4)+3(-5)^(3)-8(-5)^(2)+5(-5)-25\\=625+3(-125)-8(25)-25-25\\=625-375-200-25-25\\=0\\`