The inequality x + 2y ≥ 3 is satisfied by which of the following points? (Select all that apply.) (1, 1) (-3, 4) (-2, 2) (5, -2)

Question

asked Jan 25, 2020 117k views

2 Answers

Natix · Answer 1 · 2020-01-28T19:38:18+0000

Answer:

First option: (1, 1)

Second option: (-3, 4)

Explanation:

Substitute each point into the inequality:

Point (1,1):

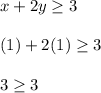
$x + 2y \geq3\\\\(1) + 2(1) \geq3\\\\3\geq3$

(The inequality is satisfied with this point)

Point (-3, 4):

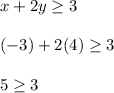
$x + 2y \geq3\\\\(-3) + 2(4) \geq3\\\\5\geq3$

(The inequality is satisfied with this point)

Point (-2, 2):

$x + 2y \geq3\\\\(-2) + 2(2) \geq3\\\\2\geq3$

(The inequality is not satisfied with this point)

Point (5, -2):

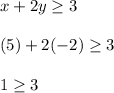
$x + 2y \geq3\\\\(5) + 2(-2) \geq3\\\\1\geq3$

(The inequality is not satisfied with this point)