Question

Gary is testing a river water sample in his lab. Initially, there are 64 bacteria in the river water sample. The number of bacteria after 3 hours can be calculated using the expression shown below.

64(1.12)3

The 3 is a exponent.

Use the given expression to complete the statements.

The quantity that represents the initial number of bacteria is ........
..
The quantity that represents the rate at which the number of bacteria is increasing is .........
which means the growth rate percentage for the bacteria is %.......l.l

Answer 1

b

Explanation:

Answer 2

Hello!

The answers are:

- The quantity that represents the initial number of bacteria is 64.

- The quantity that represents the rate at which the number of bacteria is increasing is (1+0.12) or 1.12 which means the growth rate percentage for the bacteria is 0.12 or (0.12*100), it will be 12%.

Why?

To solve the problem, and complete the statements, we need to remember the form of the exponential growth.

The exponential growth formula is given by the following formula:

`P(t)=StartAmount(1+PercentageRate)^(t)`

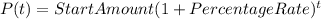
Where,

Start Amount, is the starting population or amount.

(1+Percentage Rate), is the increasing rate

Percentage Rate, is the growth rate percentage.

t, is the time elapsed.

Now, we are given the following expression:

`P(3)=64(1.12)^(3)`

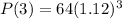
Which can be rewrited as:

`P(3)=64(1+0.12)^(3)`

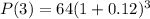
So, we have that:

- The quantity that represents the initial number of bacteria is 64.

- The quantity that represents the rate at which the number of bacteria is increasing is (1+0.12) or 1.12 which means the growth rate percentage for the bacteria is 0.12 or (0.12*100), it will be 12%.

Have a nice day!