Answer: The height of the container is 10 centimeters. If its diameter and height were both doubled, the container's capacity would be 8 times its original capacity.
Explanation:
The volume of a cone can be calculated with this formula:
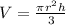
Where "r" is the radius and "h" is the height.
We know that the radius is half the diameter. Then:
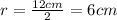
We know the volume and the radius of the conical container, then we can find "h":
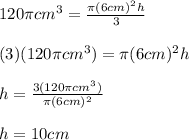
The diameter and height doubled are:
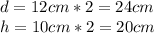
Now the radius is:
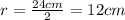
And the container capacity is
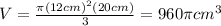
Then, to compare the capacities, we can divide this new capacity by the original:
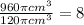
Therefore, the container's capacity would be 8 times its original capacity.