Answer: 1.011 eV
Step-by-step explanation:
The described situation is the photoelectric effect, which consists of the emission of electrons (electric current) that occurs when light falls on a metal surface under certain conditions.
If we consider the light as a stream of photons and each of them has energy, this energy is able to pull an electron out of the crystalline lattice of the metal and communicate, in addition, a kinetic energy.
This is what Einstein proposed:
Light behaves like a stream of particles called photons with an energy
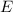 :
:
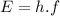 (1)
(1)
So, the energy
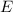 of the incident photon must be equal to the sum of the Work function
of the incident photon must be equal to the sum of the Work function
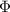 of the metal and the kinetic energy
of the metal and the kinetic energy
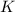 of the photoelectron:
of the photoelectron:
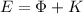 (2)
(2)
Where
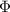 is the minimum amount of energy required to induce the photoemission of electrons from the surface of a metal, and its value depends on the metal.
is the minimum amount of energy required to induce the photoemission of electrons from the surface of a metal, and its value depends on the metal.
In this case
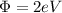 and
and

So, for the first light source of wavelength
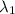 , and applying equation (2) we have:
, and applying equation (2) we have:
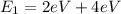 (3)
(3)
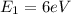 (4)
(4)
Now, substituting (1) in (4):
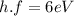 (5)
(5)
Where:
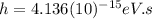 is the Planck constant
is the Planck constant
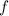 is the frequency
is the frequency
Now, the frequency has an inverse relation with the wavelength
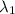 :
:
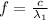 (6)
(6)
Where
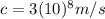 is the speed of light in vacuum
is the speed of light in vacuum
Substituting (6) in (5):
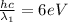 (7)
(7)
Then finding
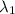 :
:
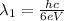 (8)
(8)
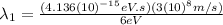
We obtain the wavelength of the first light suorce
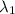 :
:
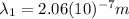 (9)
(9)
Now, we are told the second light source
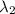 has the double the wavelength of the first:
has the double the wavelength of the first:
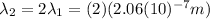 (10)
(10)
Then:
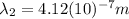 (11)
(11)
Knowing this value we can find
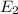 :
:
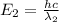 (12)
(12)
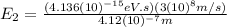 (12)
(12)
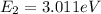 (13)
(13)
Knowing the value of
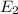 and
and
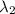 , and knowing we are working with the same work function, we can finally find the maximum kinetic energy
, and knowing we are working with the same work function, we can finally find the maximum kinetic energy
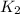 for this wavelength:
for this wavelength:
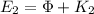 (14)
(14)
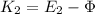 (15)
(15)
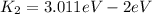
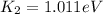 This is the maximum kinetic energy for the second light source
This is the maximum kinetic energy for the second light source