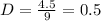Answer:
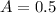

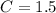

Step-by-step explanation:
The form an the equation of inverse variation is:
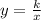
Being "k" the constant of variation.
Since we know "k" and we have the values given in the table, we can find the missing values:
To find A we need to substitute the
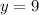 , the value of "k" and
, the value of "k" and
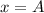 into the equation and solve for "A":
into the equation and solve for "A":
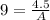
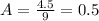
To find B we need to substitute the
 , the value of "k" and
, the value of "k" and
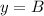 into the equation:
into the equation:
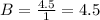
To find C we need to substitute the
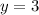 , the value of "k" and
, the value of "k" and
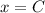 into the equation and solve for "C":
into the equation and solve for "C":
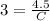
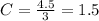
To find D we need to substitute the
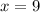 , the value of "k" and
, the value of "k" and
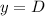 into the equation:
into the equation: