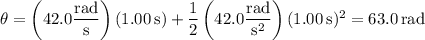With constant angular acceleration
 , the disk achieves an angular velocity
, the disk achieves an angular velocity
 at time
at time
 according to
according to
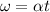
and angular displacement
 according to
according to

a. So after 1.00 s, having rotated 21.0 rad, it must have undergone an acceleration of
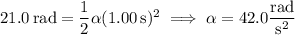
b. Under constant acceleration, the average angular velocity is equivalent to
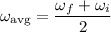
where
 and
and
 are the final and initial angular velocities, respectively. Then
are the final and initial angular velocities, respectively. Then
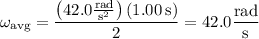
c. After 1.00 s, the disk has instantaneous angular velocity
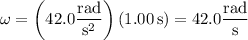
d. During the next 1.00 s, the disk will start moving with the angular velocity
 equal to the one found in part (c). Ignoring the 21.0 rad it had rotated in the first 1.00 s interval, the disk will rotate by angle
equal to the one found in part (c). Ignoring the 21.0 rad it had rotated in the first 1.00 s interval, the disk will rotate by angle
 according to
according to
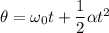
which would be equal to