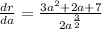Answer:
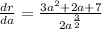
General Formulas and Concepts:
Pre-Algebra
Algebra I
- Expand by FOIL (First Outside Inside Last)
- Terms/Coefficients/Degrees
Algebra II
- Exponential Rule:
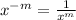
- Exponential Rule:
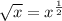
Calculus
Derivatives
Derivative Notation
The derivative of a constant is equal to 0
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Quotient Rule:
![\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))](https://img.qammunity.org/2022/formulas/mathematics/high-school/hrfl3gpx3dh352g7a9uj6guyxz9uxwhvl3.png)
Explanation:
Step 1: Define
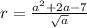
Step 2: Rewrite
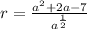
Step 3: Differentiate
- Quotient Rule [Basic Power:
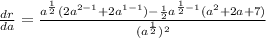
- Simplify:
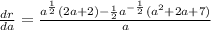
- Simplify:
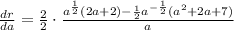
- Multiply:
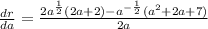
- Factor:
![(dr)/(da) = \frac{a^{-(1)/(2)}[2a(2a + 2) - (a^2 + 2a + 7)]}{2a}](https://img.qammunity.org/2022/formulas/mathematics/high-school/aaffdc128kf7qmjla7dycpskd04yppuawz.png)
- [Brackets] Distribute:
![(dr)/(da) = \frac{a^{-(1)/(2)}[4a^2 + 4a - a^2 - 2a - 7]}{2a}](https://img.qammunity.org/2022/formulas/mathematics/high-school/ywup41ur7l8g3s65zk2s0dezhuylt9usim.png)
- [Brackets] Combine Like Terms:
![(dr)/(da) = \frac{a^{-(1)/(2)}[3a^2 + 2a - 7]}{2a}](https://img.qammunity.org/2022/formulas/mathematics/high-school/r8rlkv50pigl0k31zjgg3vu4olequotrp1.png)
- Simplify: