In all cases, if
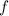 has real coefficients, then any complex roots occur in conjugate pairs, so if
has real coefficients, then any complex roots occur in conjugate pairs, so if
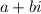 is a root, then so is
is a root, then so is
 . Also, by the fundamental theorem of algebra, if
. Also, by the fundamental theorem of algebra, if
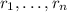 are roots to
are roots to
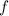 , then for some constant
, then for some constant
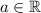 ,
,
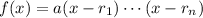
1. If
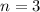 and
and
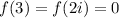 , then
, then
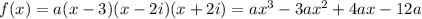
Given that
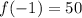 , we have
, we have
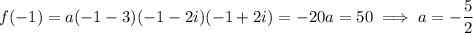
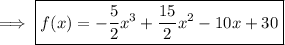
2.
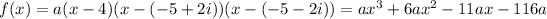
With
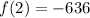 , we have
, we have
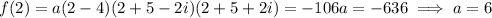
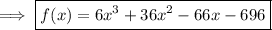
The rest are done in the same exact way.