Answer:
x² - 4x + 4
x² + 10x + 25
Explanation:
Hello!
Trinomials are polynomials with 3 terms, hence "tri".
Perfect square trinomials are the result of multiplying a binomial (2 terms) by itself, making it a square of a binomial.
Finding Perfect Square Trinomials
We can easily remove the first two solutions, as they only have two terms.
We can factor in the other three and see if the binomials as the factors are the same.
x² - 4x + 4
- x² - 4x + 4
- x² - 2x - 2x + 4
- x(x - 2) - 2(x - 2)
- (x - 2)(x - 2)
- (x - 2)²
This is a perfect square trinomial.
x² + 10x + 25
- x² + 10x + 25
- x² + 5x + 5x + 25
- x(x + 5) + 5(x + 5)
- (x + 5)(x + 5)
- (x + 5)²
This is a perfect square trinomial.
x² + 15x + 36
- x² + 15x + 36
- x² + 3x + 12x + 36
- x(x + 3) + 12(x + 3)
- (x + 12)(x + 3)
This is NOT a perfect square trinomial.
Another Method...
We can also check if a trinomial is a square by using a simple checklist.
Perfect Square Trinomial:
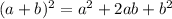
- The first term should be a perfect square
- The last term should be a perfect square (don't include the sign)
- The middle term is the square root of the last term, and then multiplied by 2
These rules only apply to polynomials with 3 terms.