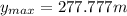Answer: 277.777 m
Step-by-step explanation:
The situation described here is parabolic movement. However, as we are told that the rock was projected upward from the surface, we will only use the equations related to the Y axis.
In this sense, the movement equations in the Y axis are:
 (1)
(1)
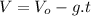 (2)
(2)
Where:
 is the rock's final position
is the rock's final position
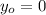 is the rock's initial position
is the rock's initial position
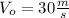 is the rock's initial velocity
is the rock's initial velocity
 is the final velocity
is the final velocity
 is the time the parabolic movement lasts
is the time the parabolic movement lasts
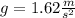 is the acceleration due to gravity at the surface of the moon
is the acceleration due to gravity at the surface of the moon
As we know
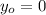 , equation (2) is rewritten as:
, equation (2) is rewritten as:
 (3)
(3)
On the other hand, the maximum height is accomplished when
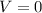 :
:
 (4)
(4)

 (5)
(5)
Finding
 :
:
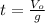 (6)
(6)
Substituting (6) in (3):
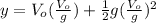 (7)
(7)
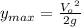 (8) Now we can calculate the maximum height of the rock
(8) Now we can calculate the maximum height of the rock
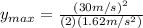 (9)
(9)
Finally: