Answer:
84%.
Explanation:
Let X be the time in minutes for a student chosen at random to finish the test.
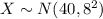 .
.
The probability that a student chosen at random finishes the test in less than 48 minutes will represented as
 .
.
Method 1: technology
Evaluate the cumulative normal probability on a calculator, where
- The lower bound is 0,
- The upper bound is 48,
- The mean
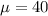 ,
, - The standard deviation

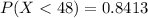 .
.
Method 2: z-score table
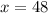 .
.
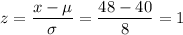 .
.
Look up the entry that corresponds to
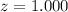 on a z-score table: 0.8413.
on a z-score table: 0.8413.
In other words,
 .
.