Question

A building manager installs sensors to see how often people turn off the lights when they leave the room. After a month the manager has a sample size of 625, a sample mean of 47%, and a sample standard deviation of 5%. What is the confidence level for a confidence interval of 46.8% to 47.2%?

A. 85%
B. 99.7%
C. 95%
D. 68%

Answer 1

Answer:D. 68

Explanation:

Answer 2

D. 68%

Explanation:

The following statistics are given;

sample mean = 47%

s = 5% ; the sample standard deviation

n = 625 ; the sample size

The confidence interval for a population mean is given as;

sample mean ± z-score*
`(s)/(√(n) )`

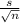
Substituting the above values we have;

47 ± z-score*
`(5)/(√(625) )`

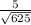
47 ± z-score*0.2

The confidence interval has been given as;

lower limit = 46.8%

upper limit = 47.2%

We can use any of these two values with the above expression to solve for the z-score. Using the lower limit we have the following equation;

47 - z-score*0.2 = 46.8

-z-score*0.2 = 46.8 - 47

-z-score*0.2 = -0.2

z-score = 1

The area of the standard normal curve between -1 and +1 will be the confidence level for the given confidence interval.

Pr( -1<Z<1 ) = 0.68 = 68%

From the Empirical rule