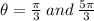ANSWER
EXPLANATION
The given trigonometric equation is:

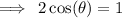
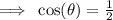
The cosine ratio is positive in the first and fourth quadrants.
In the first quadrant,

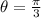
In the fourth quadrant,
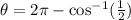
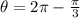

Therefore on the interval, [0,2π] the solution to the given trigonometric equation is: