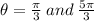Question

Find all solutions of the equation in the interval [0, 2 pi) 2 cos0-1=0

Answer 1

θ = π/3, 5π/3

Explanation:

2 cos θ - 1 = 0

2 cos θ = 1

cos θ = 1/2

θ = π/3, 5π/3

Answer 2

EXPLANATION

The given trigonometric equation is:

`2 \cos( \theta) - 1 = 0`

`\implies \: 2 \cos( \theta) = 1`

`\implies \: \cos( \theta) = (1)/(2)`

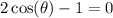
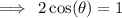
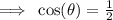
The cosine ratio is positive in the first and fourth quadrants.

In the first quadrant,

`\theta = \cos ^( - 1) ( (1)/(2))`

`\theta = (\pi)/(3)`

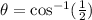
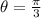
In the fourth quadrant,

`\theta =2 \pi - \cos ^( - 1) ( (1)/(2))`

`\theta =2 \pi - (\pi)/(3)`

`\theta = (5\pi)/(3)`

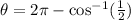
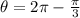
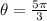
Therefore on the interval, [0,2π] the solution to the given trigonometric equation is:

`\theta = (\pi)/(3) \: and \: (5\pi)/(3)`