Question

A game called "small poker" is played with a standard deck of 52 playing cards (no jokers). In "small poker," each player is dealt four

cards (called a "hand").
(a) How many four-card hands are possible?
Answer:
(b) How many four-card hands consisting of four hearts are possible?
Answer:
(c) How many four-card hands consisting of four aces are possible?.
Answer:
(d) How many four-card hands consisting of two pairs are possible? Hint: two pairs cannot create a "four of a kind" combination
Answer:

Answer 1

a. From 52 total cards, you're drawing 4:

`\dbinom{52}4=(52!)/(4!(52-4)!)=270,725`

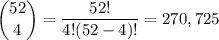
b. There are 13 hearts in the deck, and you want all 4 to be drawn from that pool. From the remaining 39, you are drawing nothing:

`\dbinom{13}4\dbinom{39}0=(13!)/(4!(13-4)!)=715`

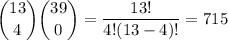
c. Similar to (b), but there are only 4 aces in the deck, and you don't care about the remaining 48 cards:

`\dbinom44\dbinom{48}0=1`

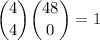
d. There are 13 ranks (ace, 2, 3, ..., 10, jack, queen, king) from which you want to draw 2. For each given rank, there are 4 possible suits, and a two of a kind consists of drawing 2 cards of the same rank, regardless of suit. Once you have two pairs, you ignore the remaining.

`\dbinom{13}2\dbinom42^2\dbinom{44}0=(13!)/(2!(13-2)!)\left((4!)/(2!(4-2)!)\right)^2=2808`

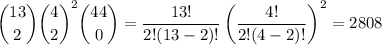
That is, there are
`\binom42^2\binom{44}0` ways of getting two pairs if the two ranks are fixed. Then you multiply this by
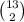`\binom{13}2`, the number of ways you can get two different ranks.