Question

The diagram shows a CD which has a radius of 6 cm. a) work out the circumference of the CD. Give your answer correct to three significant figures. CDs of this size are cut from rectangular sheets of plastic . Each sheet is 1 meter long and 50 cm wide. 

b) Work out The greatest number of CDs which can be cut from one rectangular sheet.

Answer 1

13 CDs can be cut from 1 m x 50 cm sheet

Explanation:

a) The circunference of the CD is represented by the following formula:

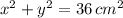`x^(2)+y^(2) = 36\,cm^(2)` (1)

Where:

`x` - Horizontal position, measured in centimeters.

`y` - Vertical position, measured in centimeters.

Now, we proceed to present a representation of the CD.

b) The area of a CD is represented by the following formula:

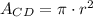`A_(CD) = \pi\cdot r^(2)` (2)

Where:

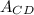`A_(CD)` - Area of the CD, measured in square centimeters.

`r` - Radius, measured in centimeters.

If we know that
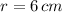`r = 6\,cm`, then the area of a CD is:

`A_(CD) = \pi\cdot (6\,cm)^(2)`

`A_(CD) = 113.097\,cm^(2)`

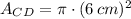
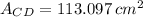
The area of the sheet is represented by this expression:

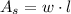`A_(s) = w\cdot l` (3)

Where:

`A_(s)` - Area of the sheet, measured in square centimeters.

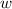`w` - Width of the sheet, measured in centimeters.

`l` - Length of the sheet, measured in centimeters.

If we know that
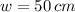`w = 50\,cm` and
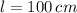`l = 100\,cm`, the area of the sheet is:

`A_(s) = (100\,cm)\cdot (50\,cm)`

`A_(s) = 1500\,cm^(2)`

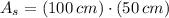
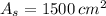
Now we divide the area of the sheet by the area of the CD:

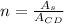`n = (A_(s))/(A_(CD))` (4)

`n = (1500\,cm^(2))/(113.097\,cm^(2))`

`n = 13.263`

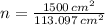
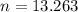
The maximum number of CD is the integer that is closer to this result. Therefore, 13 CDs can be cut from 1 m x 50 cm sheet.