Find the polynomial that represents the area of a rhombus whose diagonals are ( 2P -4) and( 2P +4)

Question

asked Nov 10, 2022 195k views

1 Answer

Clemens Sielaff · Answer 1 · 2022-11-14T23:07:16+0000

Answer:

The polynomial that represents the area of a rhombus is
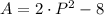$A = 2\cdot P^(2)-8$ .

Explanation:

The area formula for the rhombus is defined below:

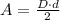$A = (D\cdot d)/(2)$ (1)

Where:

- Area of the rhombus.

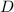- Greater diagonal.

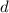- Lesser diagonal.

If we know that
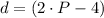$d = (2\cdot P -4)$ and
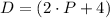$D = (2\cdot P + 4)$ , then the area formula of the rhombus:

$A = ((2\cdot P - 4)\cdot (2\cdot P +4))/(2)$

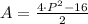
$A = (4\cdot P^(2)-16)/(2)$

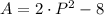
$A = 2\cdot P^(2)-8$

The polynomial that represents the area of a rhombus is
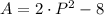$A = 2\cdot P^(2)-8$ .