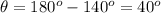Answer:
40°
Explanation:
An exterior angle and an interior angle are supplementary angles.
Two Angles are Supplementary when they add up to 180°.
Therefore the measure of exterior angle is equal to different between 180° and an interior angle.
Method 1:
You can use the formula of the measure of interior angle of the regular polygon with n-sides:
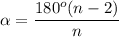
We have a nonagon. Therefore n = 9. Substitute:
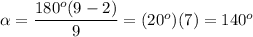
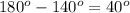
Method 2:
Look at the picture.
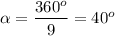
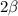 - it's an interior angle
- it's an interior angle
We know: The sum of measures of these three angles of any triangle is equal to 180°.
Therefore:
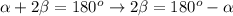
Substitute:
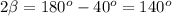
 - it's a exterior angle
- it's a exterior angle
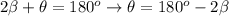
substitute: