Answer:
Approximately
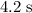 (assuming that the projectile was launched at angle of
(assuming that the projectile was launched at angle of
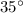 above the horizon.)
above the horizon.)
Step-by-step explanation:
Initial vertical component of velocity:
 .
.
The question assumed that there is no drag on this projectile. Additionally, the altitude of this projectile just before landing
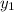 is the same as the altitude
is the same as the altitude
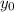 at which this projectile was launched:
at which this projectile was launched:
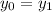 .
.
Hence, the initial vertical velocity of this projectile would be the exact opposite of the vertical velocity of this projectile right before landing. Since the initial vertical velocity is
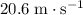 (upwards,) the vertical velocity right before landing would be
(upwards,) the vertical velocity right before landing would be
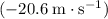 (downwards.) The change in vertical velocity is:
(downwards.) The change in vertical velocity is:
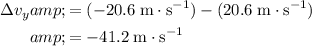 .
.
Since there is no drag on this projectile, the vertical acceleration of this projectile would be
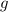 . In other words,
. In other words,
 .
.
Hence, the time it takes to achieve a (vertical) velocity change of
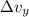 would be:
would be:
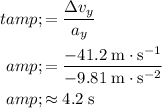 .
.
Hence, this projectile would be in the air for approximately
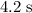 .
.