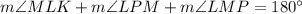Let P be a point outside the circle such that triangle LMP has legs coincident with chords MW and LK (i.e. M, W, and P are colinear, and L, K, and P are colinear). By the intersecting secants theorem,
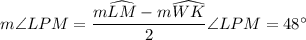
The angles in any triangle add to 180 degrees in measure, and
 and
and
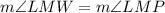 , so that
, so that